一、基本思想
数组的一大优点就是给出索引可以立刻给出其中存储的值,而散列表(Hash Table)是普通数组的推广。散列表同样可以在 \(O(1)\) 的时间内完成插入、搜索和删除的功能,但是不再要求索引是连续的数字,可以是字符串或是其他的数据结构。
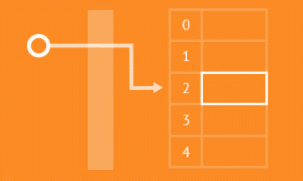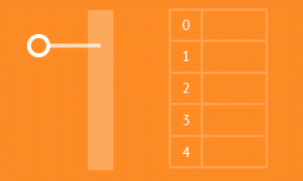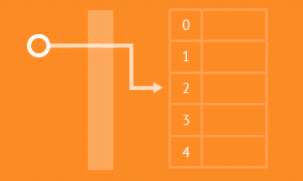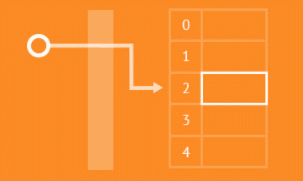
理想的散列表仍是一个固定大小的数组,只不过其包含了关键词 (key) ,每一个位置称为一个单元或者 槽(slot)。然后如上图所示,每个关键词会通过散列函数(Hash Function)映射到对应的单元,得到需要的值 (value)。传统的数组就是散列表的特殊情况,其关键词就是其索引,散列函数没有任何特殊操作,只是 1 对应 1 , 2 对应 2 而已。
以上就是散列表的基本思想,显然建立一个散列表核心问题是 散列函数的设计 。同时,如果想让所有关键词等能有对应的槽,那么整个表就会是关键词全域的大小,但往往全域极大,会占用大量的空间,所以还需 考虑全域大小。表大小比全域小就意味着两个不同关键词可能会被映射到同一个单元,这种情况称为 冲突 (collision),也是散列表设计时的一个问题。
二、散列函数
散列函数用于将关键词映射到对应的单元。为了保证散列表能够拥有良好的性能,应当尽量保证每个关键词能够被 均匀 分配到每一个单元中,同时与已被散列的关键词无关。
很多情况下,关键词并非是数字,更多的可能是字符串,所以我们可以寻找一个方法把关键词转换为自然数,然后再可以使用下面的这些方法。
除法散列法
除法散列法通过取关键词 k 除以槽数 m 的余数得到所映射到的单元编号,所以散列函数为
\[h(k)=k\ mod\ m\]对于 m 的取值,应当尽量避免 2 的 n 次幂,因为这样 \(h(k)\) 的结果就是 k 的最后 n 位(在 2 进制中),这样对于前面的几位就没有进行考虑,除非能够保证最后 n 位时等可能排列的,否则就不是一个好的散列函数。为了解决这一问题,m 选择为一个素数是一个比较好的选择。
同时要保证 m 不能过大,否则不能很好的分配的关键词。比如如果以一个字符串的所有字符 ASCII 码之和作为关键词,那么其范围在 0 - 1016 (127*8),而如果 m 选择为 10007,那很显然这种分配并不均匀。
乘法散列法
乘法散列法有两个步骤,先将关键词 k 乘上一个常数 A (0<A<1),取其小数部分乘以 m 再向下取整。散列函数为:
\[h(k)=\lfloor m(kA\ mod\ 1)\rfloor\]这一方法对于 m 的取值选择并不敏感,但更偏好 2 的 n 次幂,因为更便于计算机计算,具体原因在此不再详述。
全域散列法
对于散列函数,最为糟糕的后果就是将所有关键词都映射到同一个单元中。遇到一些特殊情况,前两种方法都会产生这一极其糟糕的后果,全域散列法采用随机的散列函数,在一组有限散列函数(称为全域的,universal)中挑选一个来避免最坏的情况产生,使其无论如何都能有良好的平均情况性能。
三、解决冲突
当插入一个元素,如果其所映射到的槽中已经有了一个元素,那么就产生了冲突,在这里介绍两种处理冲突的方法。
分离链接法
分离链接法(Separate Chaining)将所有映射到同一个槽中都存放于其中,并用一个链表保存。
只需要配合链表的相关操作就可以完成散列表所要求的操作。一般选择将新的元素插入到链表的前端,操作方便的同时,也因为新插入的元素往往在最近会更频繁的使用到,可以提高效率。
装载因子
装载因子(load factor)用来表示一个链表中平均存储元素数,即
\[\alpha = \frac{n}{m}\]其中 \(n\) 表示存储的元素数,\(m\) 表示散列表的大小。利用装载因子可以证明所有操作可以在常数时间完成,在这不展开叙述。
开放寻址法
开放寻址法(Open Addressing)仍将所有元素存放于散列表中,不引入如分离链接法中的链表和指针。主要思想是在面对冲突时,会寻找下一个槽,直到可以被放下为止。对于一个关键词,不断计算所产生的一个序列,称为 探查序列。
对于这种想法,要保证 均匀散列(Uniform Hashing)的假设,即对于每个关键词的探查序列都必须是 \(<0,1,\cdots,m-1>\) 的全排列之一,从而保证每个关键词能被均匀且一定能找到存放的位置。然而在实际应用中,并不存在完全符合这一假设的,只能采用近似的方法,常见的有如下三种:线性探查、二次探查和双重探查。
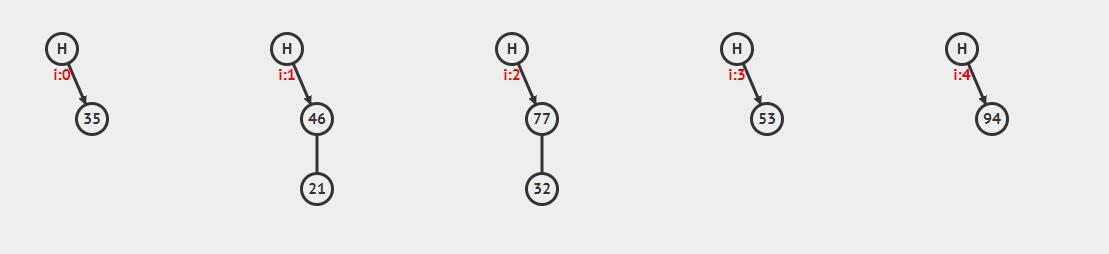
线性探查
这一方法首先需要一个普通的散列函数 \(h'\) 作为辅助散列函数(Auxiliary Hash Function),线性探查所采用的散列函数为:
\[h(k,i)=(h'(k)+i)\ mod\ m,\ \ \ \ i=0,1,\cdots,m-1\]由上一函数可以看出,对于一个确定的 \(k\) ,\(h'(k)\) 便确定,之后再偏移 \(i\) 个来寻找一个开放的位置。又因为 \(i\in[\ 0,m-1\ ]\),所以保证了均匀分布于整个范围内同时只会出现一次。

上图演示了遇到冲突时添加的过程,同时也表现出他的问题—— 一次群集 (Primary Clustering)。随着被占用的槽不断增多,出现连续被占用的槽,从而导致平均查找时间也会随之增加,称为群集现象。
二次探查
二次探查(Quadratic Probing)与一次探查一样需要一个辅助探查序列 \(h'\) ,采用如下的函数:
\[h(k,i)=(h'(k)+c_1 i+c_2 i^2 )\ mod\ m\]其中 \(c_1\) 和 \(c_2\) 为辅助常数。这一方式探查效果比一次探查好得多,但是为了能够保证充分利用散列表,\(c_1,c_2,m\) 的值需要特意去设计。
一个关键词的探查序列完全依赖于 \(h'(k)\) ,如果有两个关键词的初始探查位置相同就可能导致他们的探查序列完全一致,从而产生另一较为轻度的群集,称为 二次群集(Secondary Clustering)。
双重散列
双重散列(Double Hashing)是用于开放寻址法中最好的方法之一,其采用如下的函数:
\[h(k,i)=(h_1(k)+ih_2(k))\ mod\ m\]其中 \(h_1,h_2\) 均为辅助散列函数。这种方法第一次探查 \(h_1(k)\) 的位置,之后每次偏移 \(h_2(k)\)。显然 \(h_2(k)\) 绝不能出现为 0 的情况,否则无法偏移去寻找合适的位置。
为了能够探查整个散列表,必须要保证 \(h_2(k)\) 和 \(m\) 互素,较为便捷的方法是 m 选择 2 的幂次,而 \(h_2\) 则保证产生奇数即可。或者是令 \(m\) 为素数,让 \(h_2(k)\) 总是返回比 \(m\) 小的数,例如
\[h_1(k) = k\ mod\ n , h_2(k) = 1 + (k\ mod\ m')\]与前两种方法最大不同的地方在于后续探查偏移量与 \(i\) 和 \(h_2(k)\) 均有关,所以探查序列不单单依赖于 \(k\),从而更好地保证了随机性,使其更接近理想的均匀散列,也是使得其成为最好的方法之一的原因。